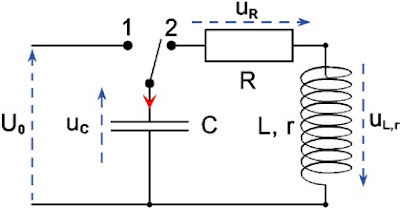
C'est un circuit "R L C" alimenté par un générateur G. Le schéma habituel d'un tel montage est représenté ci-dessous.
On a :
U = UR + UL + UC ⇒ U = RI + jLωI + I/ jCω ⇒ U = I(R + jLω +1/ jCω)
Puisque U = Z I alors on peut déduire que l’impédance est : Z = R + jLω + 1/ jCω.
Le module de Z est donné par : Z =R^2 + (Lω− 1/ Cω )^2, la phase de l’impédance est donnée par :
φ = arctan (Lω− 1 /Cω)
I- Régime Libre du circuit RLC série :
On constitue un circuit RLC en associant en série :
- un résistor de résistance R,
- un condensateur de capacité C,
- une bobine d’inductance L et de résistance r.
On s’intéresse à l’évolution de la charge q(t) du condensateur au cours du temps.
On peut faire une étude à l’oscilloscope, dans ce cas, on utilise un G.B.F. qui génère une tension en créneaux.
L’évolution de q(t) est donnée par celle de uC(t) = C1.q(t) à une constante multiplicative 1/C près.
On suit également l’évolution de i(t) qui est identique à celle de uR(t) = R.i(t), à une constante multiplicative R près : on branche la masse de l’oscilloscope en N, le générateur étant à "masse flottante". Il faut inverser le signal de la voie YB.
Il est possible de faire une étude de la "décharge" oscillante du condensateur à l’aide d’un ordinateur, en utilisant un générateur de tension continue E.
II- Oscillations Libres :
On dit qu’un circuit RLC série est en régime libre lorsqu’il ne subit aucun apport d’énergie après l’instant initial.
Sur l’écran de l’oscilloscope, on observe des oscillations amorties de uC(t) qui représentent la "charge" oscillante, puis la "décharge" oscillante du condensateur.
Pour une inductance L, et une capacité C fixées, on observe trois régimes différents de l’évolution de uC(t) suivant la valeur de la résistance Rtot = R + r.
Pour de faibles valeurs de Rtot, la tension uC(t) présente des oscillations amorties, c’est le régime pseudo-périodique
La durée entre deux passages successifs par une valeur nulle, avec une pente de même signe est la pseudo-période T des oscillations amorties. . uC(t) passe périodiquement par des valeurs nulles.
L’amplitude des oscillations de uC(t) et de uR(t) décroît au cours du temps.
On remarque que uC(t) est en retard de T/4 par rapport à uR(t) : quand uR(t) est maximum, uC(t) s’annule en croissant. Quand uR(t) s’annule en décroissant uC(t) est maximum.
Pour d’importantes valeurs de Rtot, la tension uC(t) s’amortit très vite, c’est le régime apériodique
On observe la décharge sans que uC(t) oscille.
Pour une valeur particulière de la résistance Rtot = 2.CL, le régime est qualifié de régime apériodique critique
Lors de ce régime uC(t) tend plus rapidement vers une valeur nulle.
Le régime apériodique critique est difficile à déterminer expérimentalement.
On ne considère que la décharge oscillante pour laquelle, à partir de t = 0, uAB(t) = 0 :
uAB(t) = uL,r(t) + uR(t) + uC(t) = 0
Avec, en convention des récepteurs :
Qu’on écrit :
(R+r)/L.duC(t)/dt est le terme d’amortissement qui détermine, pour L et C fixés, le type de régime (pseudo-périodique, apériodique, critique).
U = UR + UL + UC ⇒ U = RI + jLωI + I/ jCω ⇒ U = I(R + jLω +1/ jCω)
Puisque U = Z I alors on peut déduire que l’impédance est : Z = R + jLω + 1/ jCω.
Le module de Z est donné par : Z =R^2 + (Lω− 1/ Cω )^2, la phase de l’impédance est donnée par :
φ = arctan (Lω− 1 /Cω)
I- Régime Libre du circuit RLC série :
On constitue un circuit RLC en associant en série :
- un résistor de résistance R,
- un condensateur de capacité C,
- une bobine d’inductance L et de résistance r.
On s’intéresse à l’évolution de la charge q(t) du condensateur au cours du temps.
On peut faire une étude à l’oscilloscope, dans ce cas, on utilise un G.B.F. qui génère une tension en créneaux.
L’évolution de q(t) est donnée par celle de uC(t) = C1.q(t) à une constante multiplicative 1/C près.
On suit également l’évolution de i(t) qui est identique à celle de uR(t) = R.i(t), à une constante multiplicative R près : on branche la masse de l’oscilloscope en N, le générateur étant à "masse flottante". Il faut inverser le signal de la voie YB.
Il est possible de faire une étude de la "décharge" oscillante du condensateur à l’aide d’un ordinateur, en utilisant un générateur de tension continue E.
II- Oscillations Libres :
On dit qu’un circuit RLC série est en régime libre lorsqu’il ne subit aucun apport d’énergie après l’instant initial.
Sur l’écran de l’oscilloscope, on observe des oscillations amorties de uC(t) qui représentent la "charge" oscillante, puis la "décharge" oscillante du condensateur.
Pour une inductance L, et une capacité C fixées, on observe trois régimes différents de l’évolution de uC(t) suivant la valeur de la résistance Rtot = R + r.
Pour de faibles valeurs de Rtot, la tension uC(t) présente des oscillations amorties, c’est le régime pseudo-périodique
La durée entre deux passages successifs par une valeur nulle, avec une pente de même signe est la pseudo-période T des oscillations amorties. . uC(t) passe périodiquement par des valeurs nulles.
L’amplitude des oscillations de uC(t) et de uR(t) décroît au cours du temps.
On remarque que uC(t) est en retard de T/4 par rapport à uR(t) : quand uR(t) est maximum, uC(t) s’annule en croissant. Quand uR(t) s’annule en décroissant uC(t) est maximum.
Pour d’importantes valeurs de Rtot, la tension uC(t) s’amortit très vite, c’est le régime apériodique
On observe la décharge sans que uC(t) oscille.
Pour une valeur particulière de la résistance Rtot = 2.CL, le régime est qualifié de régime apériodique critique
Lors de ce régime uC(t) tend plus rapidement vers une valeur nulle.
Le régime apériodique critique est difficile à déterminer expérimentalement.
On ne considère que la décharge oscillante pour laquelle, à partir de t = 0, uAB(t) = 0 :
uAB(t) = uL,r(t) + uR(t) + uC(t) = 0
Avec, en convention des récepteurs :
uR(t) = R.i(t) ; uL,r(t) = r.i(t) + L.di(t)/dt ; q(t) = C.uC(t).
D’autre part
i(t) = dq/dt(t) = C.duC(t)/dt
et
di(t)/dt = d^2q(t)/dt^2= Cd^2uC/dt^2
D’où
L.Cd^2uC(t)/dt^2+ (R + r).C.duC(t)/dt+ uC(t) = 0
Qu’on écrit :
d^2uC(t)/dt+ (R+r)/L.duC(t)/dt+ 1/LCuC(t) = 0
(R+r)/L.duC(t)/dt est le terme d’amortissement qui détermine, pour L et C fixés, le type de régime (pseudo-périodique, apériodique, critique).




Commentaires
Enregistrer un commentaire